写在前面

最初是想要把传统的柱状频谱图做成平滑曲线连接的，“呼吸”效果应该会更自然

之前试过了最小二乘法曲线拟合，结论是最小二乘法曲线拟合不能解决这个问题：

• 最小二乘法曲线拟合：可以求出一条直线/n次曲线，把所有散点均匀地分为两部分

• 贝塞尔曲线：可以求出一条曲线平滑穿过各个散点

一.问题重述

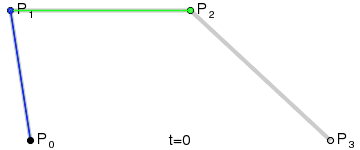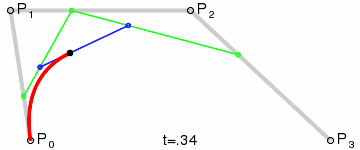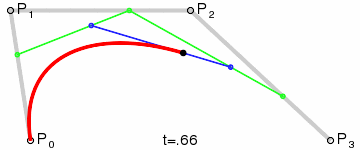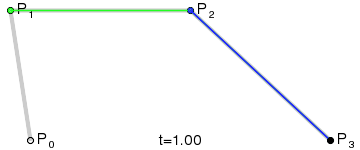
三次贝塞尔曲线需要2个控制点，如下图：

（图中的P1, P2是控制点）

通过Audio API可以获取各个散点（柱状频谱图的各个柱子的顶端），而难点就是求2个控制点，随便定是肯定不行的，效果会非常差

二.解决方案

找到了一个基于经验实践的解决方案，没有严格的数学依据，但实际效果很完美，具体步骤如下：

1. 假设控制点在(x1,y1)和(x2,y2)之间，第一个点和最后一个点分别是曲线路径上的上一个点和下一个点

2. 求中点

3. 求各中点连线长度

4. 求中点连线长度比例（用来确定平移前p2, p3的位置）

5. 平移p2

6. 平移p3

7. [可选]微调控制点与顶点之间的距离，越大曲线越平直

更多详细介绍请查看Interpolation with Bezier Curves A very simple method of smoothing polygons

平滑的效果可以看简书：Android手写优化-更为平滑的签名效果实现

三.JavaScript求三次贝塞尔曲线的控制点

原版是Java实现，笔者做了简单修改封装，如下：

window.Bezier = {
    /**
     * 获取控制点坐标
     * @param  {Array} arr 4个点坐标数组
     * @param  {Float} smooth_value [0, 1] 平滑度
     *   p1 上一个点
     *   p2 左端点
     *   P3 右端点
     *   p4 下一个点
     * @return {Array}     2个点坐标数组
     */
    getControlPoints: function(arr, smooth_value) {
        var x0 = arr[0].x, y0 = arr[0].y;
        var x1 = arr[1].x, y1 = arr[1].y;
        var x2 = arr[2].x, y2 = arr[2].y;
        var x3 = arr[3].x, y3 = arr[3].y;

        // Assume we need to calculate the control
        // points between (x1,y1) and (x2,y2).
        // Then x0,y0 - the previous vertex,
        //      x3,y3 - the next one.
        // 1.假设控制点在(x1,y1)和(x2,y2)之间，第一个点和最后一个点分别是曲线路径上的上一个点和下一个点

        // 2.求中点
        var xc1 = (x0 + x1) / 2.0;
        var yc1 = (y0 + y1) / 2.0;
        var xc2 = (x1 + x2) / 2.0;
        var yc2 = (y1 + y2) / 2.0;
        var xc3 = (x2 + x3) / 2.0;
        var yc3 = (y2 + y3) / 2.0;

        // 3.求各中点连线长度
        var len1 = Math.sqrt((x1-x0) * (x1-x0) + (y1-y0) * (y1-y0));
        var len2 = Math.sqrt((x2-x1) * (x2-x1) + (y2-y1) * (y2-y1));
        var len3 = Math.sqrt((x3-x2) * (x3-x2) + (y3-y2) * (y3-y2));

        // 4.求中点连线长度比例（用来确定平移前p2, p3的位置）
        var k1 = len1 / (len1 + len2);
        var k2 = len2 / (len2 + len3);

        // 5.平移p2
        var xm1 = xc1 + (xc2 - xc1) * k1;
        var ym1 = yc1 + (yc2 - yc1) * k1;

        // 6.平移p3
        var xm2 = xc2 + (xc3 - xc2) * k2;
        var ym2 = yc2 + (yc3 - yc2) * k2;

        // Resulting control points. Here smooth_value is mentioned
        // above coefficient K whose value should be in range [0...1].
        // 7.微调控制点与顶点之间的距离，越大曲线越平直
        var ctrl1_x = xm1 + (xc2 - xm1) * smooth_value + x1 - xm1;
        var ctrl1_y = ym1 + (yc2 - ym1) * smooth_value + y1 - ym1;

        var ctrl2_x = xm2 + (xc2 - xm2) * smooth_value + x2 - xm2;
        var ctrl2_y = ym2 + (yc2 - ym2) * smooth_value + y2 - ym2;

        return [{x: ctrl1_x, y: ctrl1_y}, {x: ctrl2_x, y: ctrl2_y}];
    }
};

注释应该比较详尽了，可以配合上面提到的Interpolation with Bezier Curves A very simple method of smoothing polygons理解

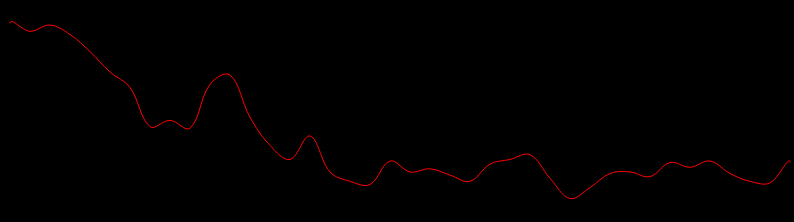
四.效果截图

平滑效果很不错，而且计算量小，能够满足实时绘图的需要（原项目是Android手写签名）

参考资料

• gcacace/android-signaturepad：原项目