Zipper_Haskell笔记13

一.不可变的数据结构

数据结构不可变，所以对其进行增、删、改等操作的结果只能是重新创建一份新的数据结构，例如：

reverse' xs
  | length xs <= 1 = xs
  | otherwise = last xs : (reverse' (init xs))

反转List就像倒序一叠扑克牌，抽出最下面的一张放到新牌堆最上方，接着抽出倒数第二张放到它下面……所以，对牌堆进行倒序操作的结果实际上是造出了一个新牌堆。新牌堆仍由之前的牌构成，但与原牌堆没有任何联系，类似于状态丢弃，直接丢掉原牌堆，而不是维护修改，例如（实现数组反转的一般方法，用JS描述）：

function swap(arr, from, to) {
  let t = arr[from];
  arr[from] = arr[to];
  arr[to] = t;
}
function reverse(arr) {
  for (let i = 0; i < arr.length / 2; i++) {
    swap(arr, i, arr.length - 1 - i);
  }
  return arr;
}

如果数据结构可变，数组反转就可以通过n/2次元素交换来实现。二者的差异在于，可变的数据结构中，我们把数据结构当做可扩展复用的容器，对数据结构的操作就是对容器里的值进行增、删、改；不可变的数据结构中，我们把数据结构当做数据常量，无法扩展和复用，所以对数据结构的操作相当于重新创建一份很像但不太一样的数据。例如swap：

swap _ _ [] = []
swap i j xs
  | i == j = xs
  | i > j = swap j i xs
  | otherwise  = (take i xs) ++ [xs !! j] ++ (sublist (i + 1) (j - 1) xs) ++ [xs !! i] ++ (drop (j + 1) xs)
  where sublist _ _ [] = []
        sublist a b xs
          | a > b = []
          | a == b = [xs !! a]
          | otherwise = (drop a . take (b + 1)) xs

一条线被2个点分成3段，List中两个元素交换的结果就是第一段并上第二个点，并上中间那段，再并上第一个点和最后一段

（摘自一场函数式思维模式的洗礼）

对应的JS描述如下（仅关键部分）：

function swap(i, j, xs) {
  return xs.slice(0, i).concat([xs[j]]).concat(xs.slice(i + 1, j)).concat([xs[i]]).concat(xs.slice(j + 1));
}

相当麻烦，而且效率也不高，比如树结构的场景，改一个节点就需要建一棵新树，再改它旁边的节点又需要创建一棵新树……简单地给所有节点值都+1就需要创建n棵完整树。实际上，局部的修改没必要重新创建整棵树，直到需要完整树的时候再去创建更合理一些。在数据结构不可变的情况下，这能实现吗？

二.在数据结构中穿梭

树

先造一颗二叉搜索树：

> let tree = fromList [7, 3, 1, 2, 6, 9, 8, 5]
> tree
Node 5 (Node 2 (Node 1 EmptyTree EmptyTree) (Node 3 EmptyTree EmptyTree)) (Node 8 (Node 6 EmptyTree (Node 7 EmptyTree EmptyTree)) (Node 9 EmptyTree EmptyTree))

（fromList及二叉搜索树的实现来自Monoid_Haskell笔记9）

树结构如下：

想要修改指定节点的话，需要知道两个东西：位置索引和新值。位置索引可以用访问路径来表示，例如：

data Direction = L | R
type Path = [Direction]

那么modify函数的类型应该是这样的：

modify :: Tree a -> Path -> Tree a -> Tree a

根据位置索引找到目标节点，换上新值即可，这样实现：

modify EmptyTree _ n = n
modify t [] n = n
modify (Node x l r) (d:ds) n
  | d == L = Node x (modify l ds n) r
  | d == R = Node x l (modify r ds n)

试玩一下，把3改成4，访问路径是[L, R]：

> modify tree [L, R] (singleton 4)
Node 5 (Node 2 (Node 1 EmptyTree EmptyTree) (Node 4 EmptyTree EmptyTree)) (Node 8 (Node 6 EmptyTree (Node 7 EmptyTree EmptyTree)) (Node 9 EmptyTree EmptyTree))

符合预期，如果改完3还想改1呢？

可以把改完3之后的完整树作为输入，再从根节点开始找到1并改成0：

> modify (modify tree [L, R] (singleton 4)) [L, L] (singleton 0)
Node 5 (Node 2 (Node 0 EmptyTree EmptyTree) (Node 4 EmptyTree EmptyTree)) (Node 8 (Node 6 EmptyTree (Node 7 EmptyTree EmptyTree)) (Node 9 EmptyTree EmptyTree))

能用，但存在2个问题：

改完3之后生成的完整树是多余的
1就是3的左兄弟，不需要再从根开始找

实际上，我们希望的是：

不生成中间多余的完整树，在需要的时候（比如一系列修改操作之后）才生成完整树
能够方便地进行局部修改（改左右兄弟、父级子级），而不用关注完整树

要对一棵子树进行多次修改，修改完毕后还要能生成完整树，怎么才能做到？

进行局部修改的同时要保留其结构上下文信息。比如修改右子树时，关注点是：

就二叉树而言，结构上下文信息由两部分组成，父节点和兄弟节点：

-- 父节点
5
-- 左兄弟
2
  1
  3

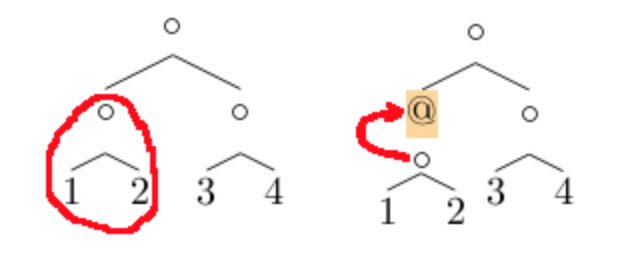
右子树加上这两部分信息，就能够得到以父节点为根的完整子树。同样，如果父节点也有其父节点和兄弟节点的信息，就能接着向上恢复子树，走到根的时候就能得到完整树。实际上，只要拥有足够的结构上下文信息，就能在树中上下左右任意穿梭，并且随时能够停下来重建完整树

先定义结构上下文信息：

data DirectionWithContext a = LeftSibling a (Tree a) | RightSibling a (Tree a) deriving (Show, Eq)
type PathWithContext a = [DirectionWithContext a]
type TreeWithContext a = (Tree a, PathWithContext a)

用LeftSibling a (Tree a)来记录结构上下文信息，其中a表示父节点的值，Tree a表示右兄弟，这是向上恢复子树所需的最小信息，一点不多余。PathWithContext与之前的Path类似，同样用来表示访问路径，只是路径的每一步除了记录方向，还记录了相应的上下文信息，包括父节点和兄弟节点

接着实现“任意穿梭”：

goLeft ((Node x l r), ps) = (l, ((LeftSibling x r) : ps))
goRight ((Node x l r), ps) = (r, ((RightSibling x l) : ps))
goUp (l, ((LeftSibling x r):ps)) = (Node x l r, ps)
goUp (r, ((RightSibling x l):ps)) = (Node x l r, ps)

走两步试玩一下，还走之前的场景，先找3，再找1，即先向左向右，再上去，最后向左：

> let cTree = (tree, [])
> let focus = goLeft (goUp (goRight (goLeft cTree)))
> fst focus
Node 1 EmptyTree EmptyTree
> snd focus
[LeftSibling 2 (Node 3 EmptyTree EmptyTree),LeftSibling 5 (Node 8 (Node 6 EmptyTree (Node 7 EmptyTree EmptyTree)) (Node 9 EmptyTree EmptyTree))]

找到了1所在子树，并且保留有完整的访问路径（5的左兄弟2的左兄弟）

要重建完整树的话，只需要原路走回到树根，这样做：

backToRoot (t, []) = (t, [])
backToRoot t = backToRoot $ goUp t

验证一下：

> fst $ backToRoot focus
Node 5 (Node 2 (Node 1 EmptyTree EmptyTree) (Node 3 EmptyTree EmptyTree)) (Node 8 (Node 6 EmptyTree (Node 7 EmptyTree EmptyTree)) (Node 9 EmptyTree EmptyTree))

能够自由穿梭，还能随时重建完整树之后，modify就变得很简单：

modifyTreeWithContext (EmptyTree, ps) _ = (EmptyTree, ps)
modifyTreeWithContext ((Node x l r), ps) v = ((Node v l r), ps)

再来一遍，先把3改成4，再把1改成0：

> let modified = modifyTreeWithContext (goLeft (goUp (modifyTreeWithContext (goRight (goLeft cTree)) 4))) 0
> fst modified
Node 0 EmptyTree EmptyTree
> fst $ backToRoot modified
Node 5 (Node 2 (Node 0 EmptyTree EmptyTree) (Node 4 EmptyTree EmptyTree)) (Node 8 (Node 6 EmptyTree (Node 7 EmptyTree EmptyTree)) (Node 9 EmptyTree EmptyTree))

与之前结果一致。看起来不太清楚，利用工具函数：

x +> f = f x
m = flip modifyTreeWithContext

简单变换一下，以更自然的方式来描述：

> fst $ backToRoot $ cTree +> goLeft +> goRight +> m 4 +> goUp +> goLeft +> m 0
Node 5 (Node 2 (Node 0 EmptyTree EmptyTree) (Node 4 EmptyTree EmptyTree)) (Node 8 (Node 6 EmptyTree (Node 7 EmptyTree EmptyTree)) (Node 9 EmptyTree EmptyTree))

从树根开始，向左走，向右走，改成4，再向上走，向左走，改成0，一系列操作相当自然，没有感受到数据结构不可变的限制

List

实际上，List也能以这种更自然的方式来操作，只要带上结构上下文信息即可

对于List来说，只有左右2个方向，比树的场景简单许多：

type ListWithContext a = ([a], [a])

左右穿梭、重建完整List、修改元素都很容易实现：

goListRight (x:xs, ps) = (xs, x:ps)
goListLeft (xs, p:ps) = (p:xs, ps)
backToHead (xs, []) = (xs, [])
backToHead ls = backToHead $ goListLeft ls
modifyListWithContext ([], ps) _ = ([], ps)
modifyListWithContext (x:xs, ps) v = (v:xs, ps)

试玩一下：

> let list = [1, 3, 5, 7, 8, 10, 12]
> let cList = (list, [])
> m = flip modifyListWithContext
> let modified = cList +> goListRight +> goListRight +> goListRight +> m 4 +> goListLeft +> goListLeft +> m 2
> modified
([2,5,4,8,10,12],[1])
> fst $ backToHead modified
[1,2,5,4,8,10,12]

把第4个元素改成了4，第2个元素改成了2。对比之前的做法：

modifyList xs i x = take i xs ++ [x] ++ drop (i + 1) xs
> modifyList (modifyList list 1 2) 3 4
[1,2,5,4,8,10,12]

二者的差异在于，前者支持以符合直觉的方式遍历、修改元素，对不可变的限制无感知

三.Zipper是什么东西

上面我们定义的TreeWithContext、ListWithContext都是Zipper，正规描述如下：

The Zipper is an idiom that uses the idea of “context” to the means of manipulating locations in a data structure.

用“上下文”的思想来处理数据结构中的位置，习惯叫法是Zipper（拉链）。为什么叫“拉链”呢？

ListWithContext就是拉链，非常形象。把List当作拉链，锁头是一个游标（cursor，或者理解成指针），游标所指的位置上的元素就是当前元素，其余元素是其上下文。锁头向右拉开，向左拉住（想象拉文件袋封口的动作），对应到数据结构操作中就是，向右访问新元素，拉到最右端就是遍历，向左访问历史元素，拉到最左端就是重建完整List

类似的，TreeWithContext也可以这样理解，向左向右拉开，访问新元素，向上拉住，访问历史元素，拉到顶部就是重建完整树

具体地，Zipper可以据其通用程度分为：

针对特定数据结构的Zipper：如ListZipper、TravelTree、TravelBTree
通用Zipper：如Zipper Monad、Generic Zipper

针对具体数据结构的Zipper我们已经实现过两个了（把xxxWithContext换成Zipper即可），大致思路是：

Zipper, the functional cursor into a data structure, is itself a data structure, derived from the original one. The derived data type D’ for the recursive data type D is D with exactly one hole. Filling-in the hole — integrating over all positions of the hole — gives the data type D back.

从给定的数据结构派生出Zipper结构，具体做法是把原数据结构拆成两部分，子结构（作为值）和带“洞”的结构（作为值的结构上下文，有“洞”是因为从原完整结构上抠掉了值所在的子结构），二者拼起来恰好就是原完整结构，如下图：

zipper-hole

Zipper Monad

The Zipper Monad is a generic monad for navigating around arbitrary data structures. It supports movement, mutation and classification of nodes (is this node the top node or a child node?, etc).

除了支持移动，修改外，还能区分节点类型。基本实现如下：

import Control.Monad.State

data Loc c a = Loc { struct :: a,
                    cxt    :: c }
            deriving (Show, Eq)

newtype Travel loc a = Travel { unT :: State loc a }
    deriving (Functor, Monad, MonadState loc, Eq)

结构 + 上下文 = 位置，通过几个monadic函数来遍历、修改：

traverse :: Loc c a            -- starting location (initial state)
        -> Travel (Loc c a) a -- locational computation to use
        -> a                  -- resulting substructure
traverse start tt = evalState (unT tt) start

-- modify the substructure at the current node
modifyStruct :: (a -> a) -> Travel (Loc c a) a
modifyStruct f = modify editStruct >> liftM struct get where
    editStruct (Loc s c) = Loc (f s) c

-- put a new substructure at the current node
putStruct :: a -> Travel (Loc c a) a
putStruct t = modifyStruct $ const t

-- get the current substructure
getStruct :: Travel (Loc c a) a
getStruct = modifyStruct id -- works because modifyTree returns the 'new' tree

P.S.本来是给Zipper设计的通用Monad，结果发现并不需要：

It’s designed for use with The Zipper but in fact there is no requirement to use such an idiom.

目前好像被当做树结构专用的了：

Zipper monad is a monad which implements the zipper for binary trees.

Generic Zipper

另一种通用Zipper：

Generic Zipper: the context of a traversal

把Zipper看做遍历操作的上下文，与之前的思路不同：

We advocate a different view, emphasizing not the result of navigating through a data structure to a desired item and extracting it, but the process of navigation.

不强调移动到数据结构中的某个位置，访问想要的东西，而只关注移动的过程：

Each data structure comes with a method to enumerate its components, representing the data structure as a stream of the nodes visited during the enumeration. To let the user focus on a item and submit an update, the enumeration process should yield control to the user once it reached an item.

从遍历的角度看，数据结构就是枚举过程中被访问到的节点形成的流。那么，要关注某个节点并更新的话，枚举过程应该在访问到该节点时把控制权交回给用户，例如：

Current element: 1
Enter Return, q or the replacement value:

Current element: 2
Enter Return, q or the replacement value:

Current element: 6
Enter Return, q or the replacement value:
42
Current element: 24
Enter Return, q or the replacement value:
q
Done:
fromList [(1,1),(2,2),(3,42),(4,24),(5,120),(6,720),(7,5040),(8,40320),(9,362880),(10,3628800)]

（具体见ZipperTraversable）

P.S.这个思路像极了JS里的生成器，每走一步都喘口气看看要不要修改元素，或者停止遍历：

As Chung-chieh Shan aptly put it, ‘zipper is a suspended walk.’

黯羽轻扬

一.不可变的数据结构

二.在数据结构中穿梭

树

List

三.Zipper是什么东西

Zipper Monad

Generic Zipper

参考资料

发表评论取消回复

一.不可变的数据结构

二.在数据结构中穿梭

树

List

三.Zipper是什么东西

Zipper Monad

Generic Zipper

参考资料

发表评论 取消回复

发表评论取消回复